️Meshan Khosla
Coffee Codex - Lamport Clocks

Coffee Codex - Lamport Clocks

Meshan Khosla,

Introduction

I’m at Toasted in Bellevue, WA and I’m learning about Logical Time (specifically Lamport Clocks) in distributed systems.

Coffee

Recap

In the last post, I learned about how systems struggle with physical time and the strategies (i.e. NTP) they use to guarantee ordering using their clocks. Today, I’ll learn about logical time which solves some of the key problems with physical time.

Context

Physical time works great for our everyday lives since we are accustomed to measuring events by the second/minute/some time interval. Logical time takes a different approach: it measures the number of events rather than the seconds elapsed. While we saw how causality can be measured using seconds in the last post, logical time is explicitly designed for causal relationships.

There are 2 types of logical clocks: Lamport and Vector. In this post, I’ll be learning about Lamport clocks.

Lamport Clocks

The Lamport clock algorithm goes like this:

  • Every node maintains its own local counter of events, t
  • t is incremented on every local event Let’s call the value of t after increment L(e) for the Lamport timestamp
  • On a network request, attach the value of t to the message
  • When a request is received from another node, the current node updates their timestamp to the received message if it is greater than the current, and then increments.

In code, this algorithm looks like this:

let t = 0;

function doLocalEvent(e) {
	eventLogic(e); // Abstracted
	t++;
}

function sendNetworkRequest(node, message) {
	t++;
	sendRequest(node, message, t); // Abstracted
}

function receiveNetworkRequest(message, senderTimestamp) {
	t = Math.max(t, senderTimestamp) + 1;
	processMessage(message) // Abstracted
}

Implications

With this algorithm, we know that if a happened before b, then L(a) is less than L(b) (a -> b) => (L(a) < L(b)) This implication is clear when you consider one Node (since Lamport time is monotonically increasing on one node). The implication applies when a Node is communicating with another Node, since the receiving node updates its t with the max + 1. However, with 2 independent nodes, the events are concurrent since there’s no implication of causality that can be made.

However, the converse is not true, (L(a) < L(b)) ⇏ (a -> b) To see this, consider the two independent nodes, it can be the case that Node A has t = 100 and Node B has not had an event yet. Then, Node B has a local event and t = 1. Even though the Lamport timestamp of B < the Lamport timestamp of A, it’s clear that Node A had 100 events prior to Node B having a single one.

Since it’s possible for two events with the same timestamp, we can uniquely identify events with a tuple of (L(e), Node) as seen in the image below:

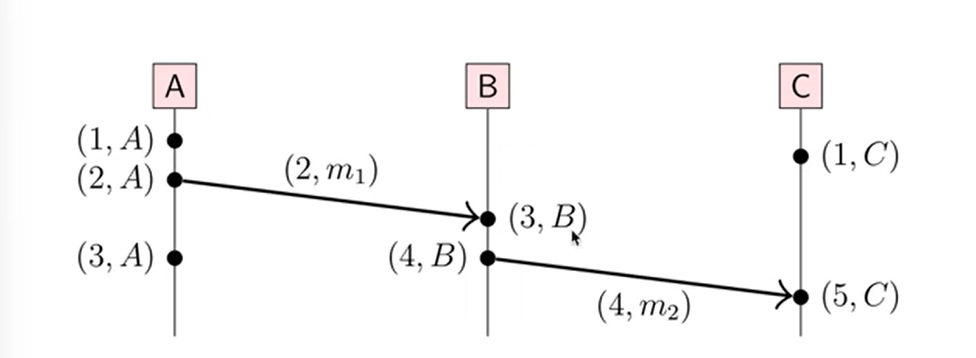
Diagram

With Lamport clocks we can define a total order: (a < b) <=> ((L(a) < L(b)) ∨ (L(a) = L(b) ∧ N(a) < N(b))) This is related to the causal order, so it’s best to thing of < as a relative happened-before with causal relationships.

Limitations

As mentioned before, a limitation to Lamport clocks is that if you’re given L(a) < L(b), we can’t tell if a -> b or a || b. Vector clocks will be used to address this limitation in the next post!

References

profile image