Union Find Implementation in Redis
Meshan Khosla,An Introduction
I really like disjoint sets. The first time I learned about them, I was fascinated. However, they’re typically in-memory and used for numbers. This is my attempt at implementing the data structure using a durable datastore.
I decided to use Redis, specifically Upstash Redis, which is a durable implementation of Redis.
Disjoint Sets / Union Find
First, we need to understand what a disjoint set, also known as a Union Find data structure, is. The two are synonymous, so I’ll refer to it as Union Find for the rest of this post.
The interface for Union Find is very simple:
union(nodeOne, nodeTwo)
areConnected(nodeOne, nodeTwo)There are, of course, variations to this (connect, isConnected, find, etc) but I’m a fan of union to union two nodes together, and areConnected to check if the two nodes are connected.
I won’t go into too much detail about the variations of Union Find, but you can read more about Quick Find and Quick Union in the CS61B textbook . In this project, we are going to implement Weighted Quick Union (WQU) with Path Compression. Here’s how it works.
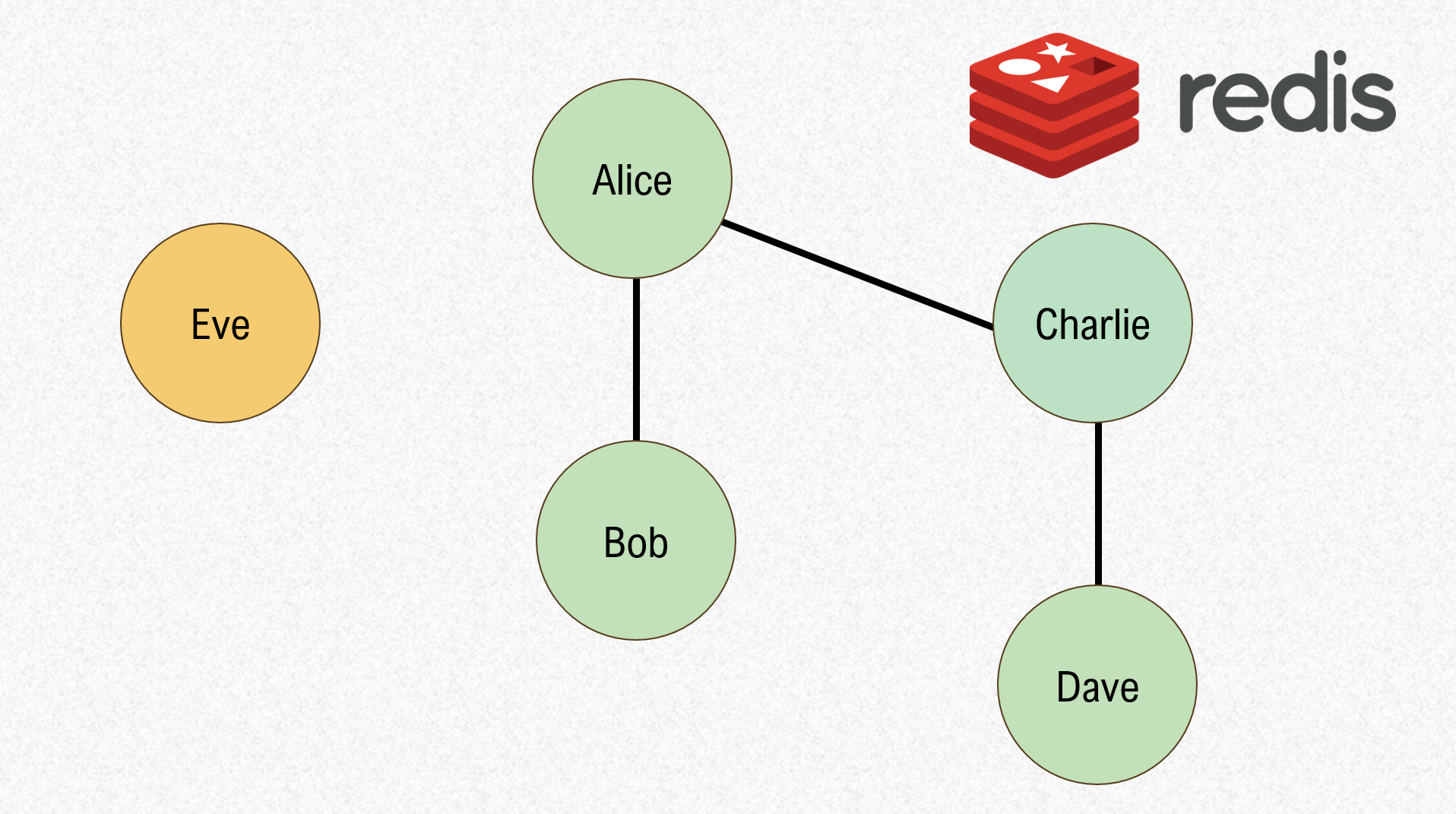
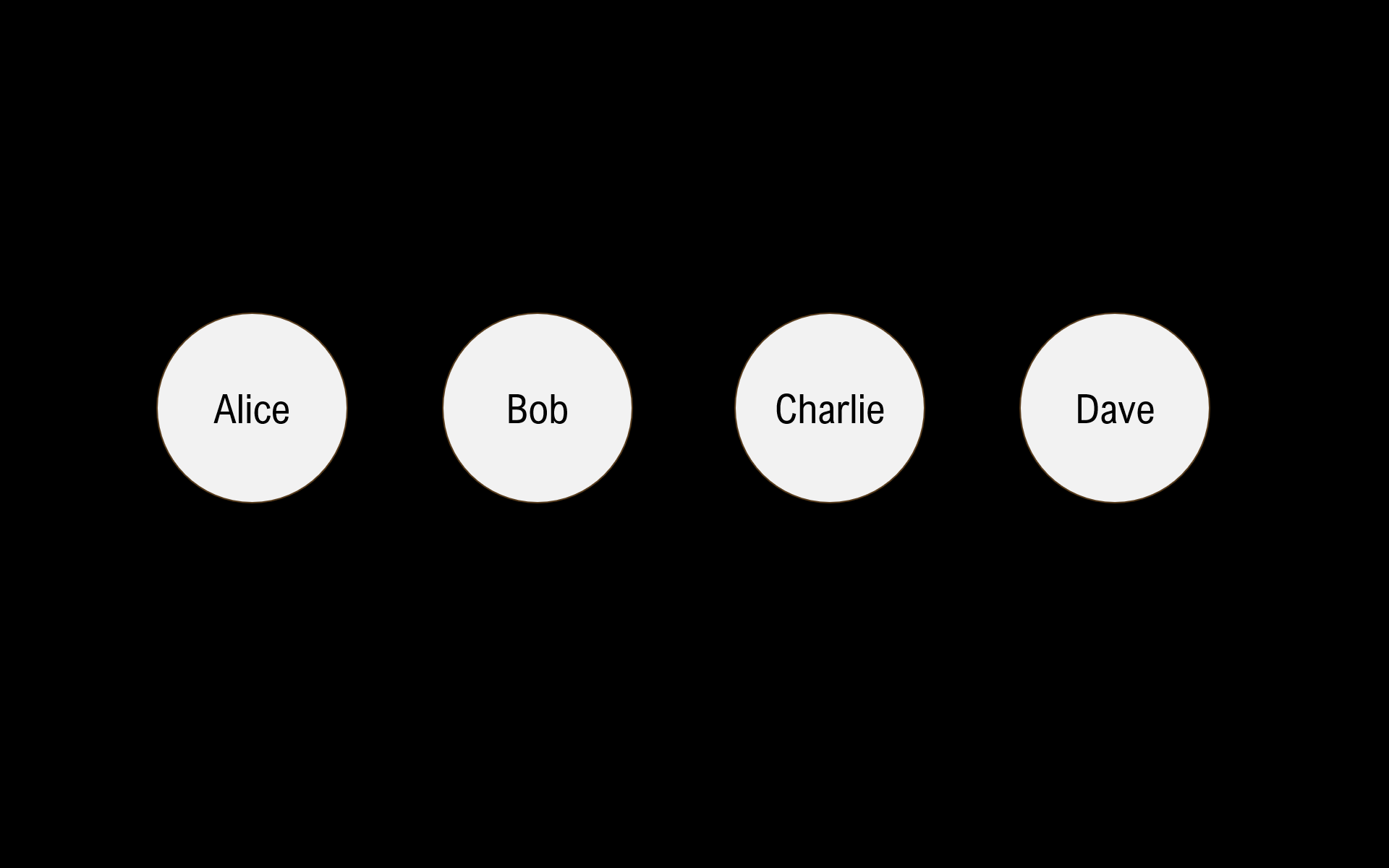
Let’s say we have 4 nodes: Alice, Bob, Charlie, and Dave.
Each node starts off alone in its own set, aka 4 disjoint sets.
Now, let’s union("Alice", "Bob"). This means Alice and Bob are now connected, and we now have 3 disjoint sets.
The way we represent this in Weighted Quick Union is by setting the larger root as the parent of the smaller root. In this case, Alice and Bob both have a size of 1, so we can arbitrarily make Alice the parent.
Now let’s union("Charlie", "Dave")
And finally union("Bob", "Charlie")
Here we can arbitrarily make Alice the parent since both sets have a size of 2.
To demonstrate WQU, let’s also union("Bob", "Eve"). Eve becomes Alice’s child since Alice is the root and has a weight of 4, which is greater than Eve’s 1. Note that we could have union’d Eve with any other node, since they all belong to the same set.
Now we’re left with 1 set and if we follow WQU, our connect and areConnected will run in logarithmic time with respect to the number of nodes!
But we can do faster with Path Compression, as we’ll see in a bit.
Implementation
A typical implementation of Union Find will be represented using a 1D array and a fixed capacity. This array can represent this tree in the following way:
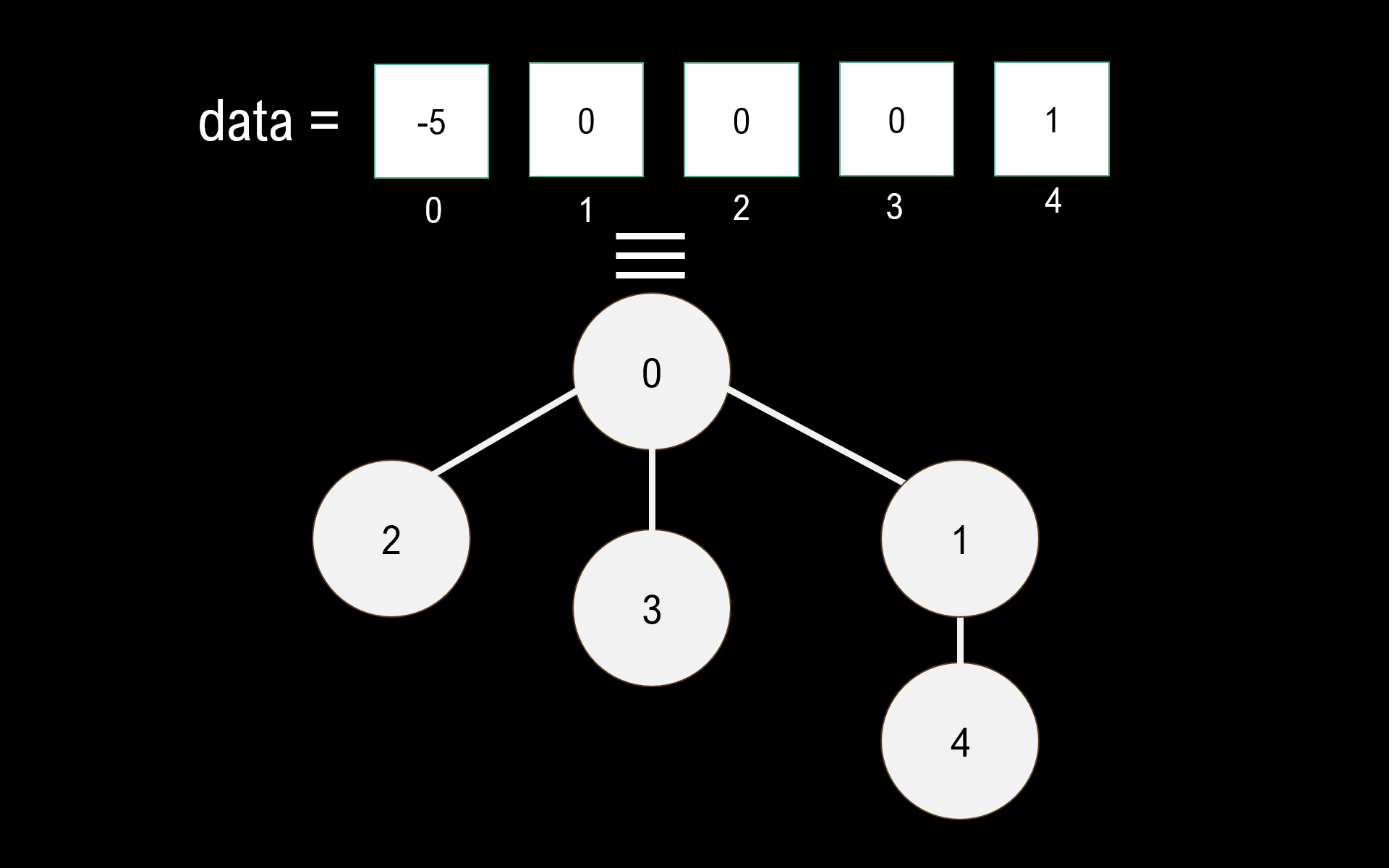
The index of the array is the element, and data[index] is the parent. We know we’re at the root of the tree when we traverse up and the parent is a negative number. This negative number represents the negated size of the set, which is necessary for WQU.
This implementation is great, but what if we want to connect arbitrary nodes, not just numbers from 0 to N-1? This is where we can use Redis hashes.
Redis Data Structure
Instead of using an array, each node can be a key in Redis, and we can map it to a hash containing that nodes parent and set size (relevant for the root).

In this implementation, the parent of the root will be itself.
Let’s get into the specific methods. I omitted error checking from these code examples so it’s a bit clearer to follow.
union(nodeOne, nodeTwo) implementation
The first thing to consider for union(nodeOne, nodeTwo) is what happens when the nodes do not exist. We could have a separate method for registering nodes, or throw an error, but I’m going to opt for simply creating the node that does not exist:
const addNodesScript = `
local nodeOne = redis.call("HGETALL", KEYS[1])
local nodeTwo = redis.call("HGETALL", KEYS[2])
if #nodeOne == 0 then
redis.call("HSET", KEYS[1], "parent", KEYS[3])
redis.call("HSET", KEYS[1], "size", 1)
end
if #nodeTwo == 0 then
redis.call("HSET", KEYS[2], "parent", KEYS[4])
redis.call("HSET", KEYS[2], "size", 1)
end
`;
await this.redis.eval(
addNodesScript
[this.getRedisKey(nodeOne), this.getRedisKey(nodeTwo), nodeOne, nodeTwo],
[]
);I opted to use a script so the nodes can be created in one network trip.
We can then find the root of each set, and set the smaller set to be the child of the bigger set. This is what the “Weighted” in WeightedQuickUnion refers to.
We’ll get back to the implementation of findRoot and note that Promise.all is used to send the requests concurrently.
The getRedisKey method is used to partition a Redis DB, so you can use the same DB for multiple projects. In our case, it adds a prefix of "!!unionfind!!--" to each key.
const [nodeOneRoot, nodeTwoRoot] = await Promise.all([
this.findRoot(nodeOne),
this.findRoot(nodeTwo),
]);
if (nodeOneRoot === nodeTwoRoot) {
return;
}
const [setOneSize, setTwoSize] = await Promise.all([
this.redis.hget<number>(this.getRedisKey(nodeOneRoot), "size"),
this.redis.hget<number>(this.getRedisKey(nodeTwoRoot), "size"),
]);
// Make smaller set a child of the bigger set
let smallerSet = setOneSize < setTwoSize ? nodeOneRoot : nodeTwoRoot;
let biggerSet = setOneSize < setTwoSize ? nodeTwoRoot : nodeOneRoot;
await this.redis.hset(this.getRedisKey(smallerSet), {
parent: biggerSet,
});
await this.redis.hset(this.getRedisKey(biggerSet), {
size: setOneSize + setTwoSize,
});Cool!
findRoot(node) implementation
But how do we actually find the root? Well each node stores a pointer to its parent in the Redis hash, so we can just traverse up with a loop.
let curNode = node;
while (true) {
const curNodeKey = this.getRedisKey(curNode);
const parent = await this.redis.hget<string>(curNodeKey, "parent");
if (parent === curNode) {
break;
}
curNode = parent;
}
return curNode;areConnected(nodeOne, nodeTwo)
Now it’s time to check if two nodes are a part of the same set. It turns out, we’ve already written the code for this.
All it takes is checking if the two nodes have the same root!
Once again, Promise.all is used to send the requests concurrently.
const [nodeOneRoot, nodeTwoRoot] = await Promise.all([
this.findRoot(nodeOne),
this.findRoot(nodeTwo),
]);
return nodeOneRoot === nodeTwoRoot;Path Compression implementation
We’ve achieved logarithmic time complexity for our methods, but can we do faster?
It turns out, yes! Traversing up the tree is logarithmic, but what if our nodes were already connected to the root of tree? The time complexity of our methods would grow with the inverse ackermann function
It’s also pretty simple to implement:
We just need to modify findRoot to keep track of each node, and then set each of their parents to the root node at the end. We can pipeline these changes so they can happen in one network request.
let curNode = node;
const toCompress = []; // New
while (true) {
const curNodeKey = this.getRedisKey(curNode);
const parent = await this.redis.hget<string>(curNodeKey, "parent");
if (parent === curNode) {
break;
}
toCompress.push(curNode); // New
curNode = parent;
}
// Compress the path by setting the parent of all nodes in the path to the root
if (toCompress.length > 0) {
const pipeline = this.redis.pipeline();
for (const node of toCompress) {
const nodeKey = this.getRedisKey(node);
pipeline.hset(nodeKey, {
parent: curNode,
});
}
await pipeline.exec();
}
return curNode;Conclusion
This project was just a random idea I had and I thought it would be fun to implement. It was! There are certainly some more possible optimizations and perhaps better design decisions, but I enjoyed it nonetheless.
See the full code on GitHub
I also decided to publish to npm, in case anyone has a practical use case for this data structure!
npm install redis-union-findconst uf = new UnionFind({
redisToken: process.env.REDIS_TOKEN!,
redisUrl: process.env.REDIS_URL!,
})
await uf.connect("Alice", "Bob")